Eine zweidimensionale Mehrfachoperation besteht aus zwei Wertereihen, somit aus "Werte aus Zeile" und "Werte aus Spalte".
Anmerkung:
Das folgende Beispiel könnte man auch mit relativer/absoluter Adressierung lösen, jedoch wurde es gewählt, um möglichst einfach die Funktionsweise einer Mehrfachoperation darzustellen.
Wir haben 3 Zahlen und führen damit die Rechenoperation (a+b)n durch. Dabei sollen die Berechnungen mit den Hochzahlen von 2 bis 10 durchgeführt werden und für eine Zahl a von 1 bis 5 .
Im Bild befinden sich die Hochzahlen in der Spalte D und die Zahlenreihe a in Zeile 6. Das erste was Sie erledigen müssen, ist die Eingabe der allgemeinen Formel:
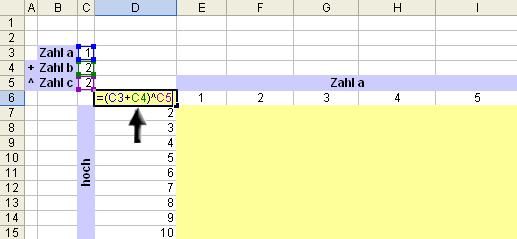
Beachten Sie bitte, wo sich die Formel für die Rechenoperation (a+b)n befindet! Diese befindet sich im Gegensatz zu einer eindimensionalen Mehrfachoperation genau im Schnittpunkt der beiden Wertereihen.
Als nächstes müssen Sie den Bereich von D6:I15 markieren, damit die Formel, die Wertereihe und auch der auszurechnende Bereich enthalten sind.

Danach wählen Sie das
Menü: Daten
Befehl: Tabelle
wodurch Sie dieses Fenster erhalten:
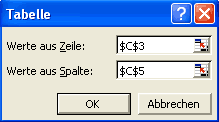
Unsere Hochzahlen befinden sich in der Spalte D. Deswegen sind sie der "Werte aus Spalte" zuzuordnen. Unsere Werte der Zahl a sind in der Zeile 5, deswegen sind sie der "Werte aus Zeile" zuzuordnen.
Bei "Werte aus Zeile" müssen Sie die Zelle C3 angeben, da sich in dieser Zelle die Zahl a befindet.
Wenn Sie den Cursor in "Werte aus Spalte" gesetzt haben, müssen Sie die Zelle C5 anklicken. Dies deshalb, weil in der Formel ist enthalten ist, dass die Hochzahlen aus der Zelle C5 entnommen werden.
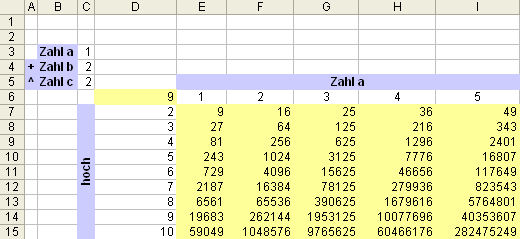
Jetzt nur mehr mit OK bestätigen und dann sollten sie folgendes Ergebnis erhalten:
|
Lehrbeispiel: Mehrfachoperation - Zweidimensional
|
||
|
Übungsbeispiel: SVerweis - Provisionen
|
||
Angabe: In der Excel Datei finden Sie folgende Absatzkalkulation:
Aufgabe: Berechnen Sie den Listenpreis für eine Matrix mit folgenden Werten: Rabatt: 5/6/7/8/9 Prozent |
||
|
|
Video nicht vorhanden |
|
